* 알아두어야할 단어
- At initiation (계약 시), At expiration (만기 시)
- FRA (Forward Rate Agreement; 선도금리계약)
- inception (시작, 개시)
- the notional (명목금액)
LOS 52.a : 선도계약의 가격결정과 가치, 다양한 시점에서의 선도계약 가치
* 선도가격의 결정 (Pricing; F(T)) = 무차익거래 조건을 만족하는 선도가격을 산출해내는 것
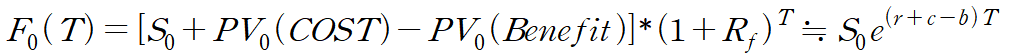
* 선도가격의 가치평가 (Valuation; V(T)) = 파생상품의 현재가치는 미래에 발생하는 Payoff의 현재가치

1) 선도계약의 가치평가
① 만기시점 (at expiration)의 선도계약 가치 = 만기시점의 지급금액(Payoff) 과 동일
- Payoff(Long position) = ST - F0(T) = VT(T) *이 만기시점의 Payoff를 현가하면 선도계약의 현재가치가 된다.
② 계약시점(at initiation) 만기시점에서 최초 계약시점 까지 현재가치로 할인을 해보자! (ST를 현가하면 S0이 된다!)
- V0(T) = S0 - F0(T)/(1+Rf)^(T)
- 여기에 앞서서 Pricing된 F0(T) = S0*(1+Rf)^(T)를 대입하면 V0(T)=0이된다.
③ 어느시점 (t)으로 응용해보면
- Vt(T) = St - F0(T)/(1+Rf)^(T-t)
* 현물보관비용이나 현물보유편익까지 고려한 식은 아래와 같다.

LOS 52.b : Forward rate(선도금리)의 결정 (기간별구조)
* Forward Rate Agreement (FRA)란?
- 미래의 일정구간 동안에 적용할 금리를 미리 약정하는 계약 (미래의 금리를 사고팔기로 약정하는 계약)
- FRA의 기초자산으로 가장 많이 활용되는 금리 : LIBOR, MRR
- FRA의 포지션
ⓐ FRA Long Position : 선도금리를 미리 사는 계약 → 미래시점에 미리 약정한 금리로 Borrowing
(금리 상승을 회피하기 위해 미래에 어떤 시점에 특정금리로 돈을 빌리려고하는 포지션)
ⓑ FRA Short Position : 선도금리를 미리 파는 계약 → 미래시점에 미리 약정한 금리로 Lending
(금리 하락을 회피하기 위해 미래에 어떤 시점에 특정금리로 돈을 빌려주려고 하는 포지션) - Notation : F(n1, n2) - n1년 후에 n2년짜리 대출
n1 = How far in the future the money will be loaned & n2 = the lengh of the loan period
F(1,3) = One-year forward, 3-year rate = a loan for the period from year 1 to year 4.
F(3,1) = Three-year forward, 1-year rate = a loan for the period from year 3 to year 4. - Implied forward rate(내재선도금리) - Forward rate for which the following two strategies have the same yield over the total period
(1) Investing from t=0 to the forward date, and rolling over the proceeds for the period of the forward.
(2) Investing from t=0 until the end of the forward period.
* Implied forward rate - the breakeven reinvestment rate linking a short-dated and long-dated zero-coupon bond.
* 현재시점에 1년짜리 금리랑 3년짜리 금리를 알고 있다고 했을 때, F(2,1)을 계산할 수 있다.
(1+Z3)^(3) = (1+Z1)^(1)(1+F(2,1))^(2)
즉, 3년짜리 금리 3년 보유 = 1년 보유 후 F(2,1)금리로 롤오버 한 수익률과 동일하다는 식으로 F(2,1)계산

- FRA Payoff = 명목금액 * (FRA 만기시점의 시장금리(MRR) - FRA 계약금리) * D/360 (개월수로 따지는 단기에는 단리로 계산함)
- 시장금리(MRR) > 계약금리(F) : FRA Long position 이익
- 시장금리(MRR) < 계약금리(F) : FRA Long position 손실 - Similar to the swap, fixed versus floating payments on an FRA occur on a net basis and the notional is not exchanged but is used soley for interest caculations.
* FRA에서 명목금액을 교환하지 않고, 현가화한 차액 차이로 결제
'CFA' 카테고리의 다른 글
| [CFA 파생상품] 55~57. Pricing and Valuation of Options, Put-Call Parity, Binomial Model (0) | 2023.11.04 |
|---|---|
| [CFA 파생상품] 53~54. Pricing and Valuation of Futures Contracts, Swaps (1) | 2023.10.29 |
| [CFA 파생상품] 51. Arbitrage, Replication, and the Cost of carry (2) | 2023.10.29 |
| [CFA 파생상품] 48~50. Derivative 기초 (1) | 2023.10.29 |
| [CFA] 43.Fixed-Income Securites: Issuance, Trading and Funding (1) | 2023.10.17 |